|
Gear Demo:
The gears are modeled and positioned in such a manner that the user can turn one gear with the other in either direction. The teeth are not so tightly interlocking that there is always a collision. In the demonstration shown, the gears contain a few hundred polygons and about 20 convex primitives. The user can attach the haptic probe to either gear in two different modes. Clicking the button towards the rim of the gear is like inserting a rod into a bicycle wheel. The probe's position remains at a fixed radius from the center of the gear and its orientation is fixed so as to rotate with the gear at that radius. If the user clicks around the center of a gear, the probe effectively becomes the gear. Its position is fixed, and it is only allowed to rotate about one axis. In this mode, the user turns the gears and feels their interactions entirely through the torque of the probe handle.
|

|
Peg-in-the-hole Demo:
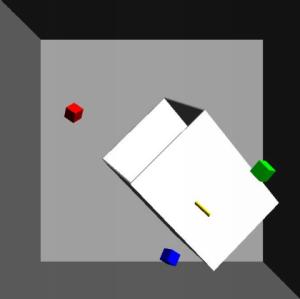
In this scenario, the user attaches the probe to a rectangular peg and attempts to insert it into a rectangular hole. Often one or two pairs of the parallel faces are the pair(s) of the closest features and may be in contact. If any type of sampling technique is used, the number of contact points would be very high, since nearly all faces of the peg are in close proximity with the walls of the hole. Collision detection and contact determination for such a seemingly simple scene are actually rather difficult, due to its contact configuration and geometric robustness problem.
|
|
Dice and shaker:
We have a dynamic scene with objects moving under the influence of gravity. There are three dice in a box-like shaker. The user can grab the shaker and influence the motion of the dice. Gravity results in the user feeling continuous force and torque and the collisions between the shaker and the dice result in impulse force and torque which are felt as small blips.
|
|
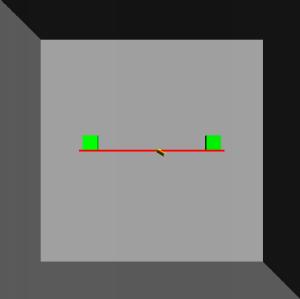
Plank and weights:
The user can manipulate a plank and a pair of cubes with unequal weights.
|
|
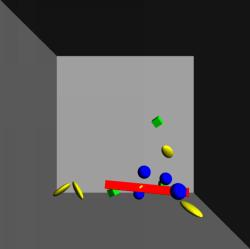
Dynamic scene of multiple moving objects:
In this setup, there are four cubes, four spheres (320 faces each), four ellipsoids (320 faces each) and a stick like block. The user can grab any object and move about interacting with the other objects.
|