BRVO: Predicting Pedestrian Trajectories using Velocity-Space Reasoning
Sujeong Kim, Stephen J. Guy, David Wilkie, Ming C. Lin, Dinesh Manocha
University of North Carolina at Chapel-Hill
Wenxi Liu, Rynson W. H. Lau
City University of Hong Kong
![]()
We introduce a novel, online method to predict pedestrian trajectories using agent-based velocity-space reasoning for improved human–robot interaction and collision-free navigation. Our formulation uses velocity obstacles to model the trajectory of each moving pedestrian in a robot’s environment and improves the motion model by adaptively learning relevant parameters based on sensor data. The resulting motion model for each agent is computed using statistical inferencing techniques, including a combination of ensemble Kalman filters and a maximum-likelihood estimation algorithm. This allows a robot to learn individual motion parameters for every agent in the scene at interactive rates. We highlight the performance of our motion prediction method in real-world crowded scenarios, compare its performance with prior techniques, and demonstrate the improved accuracy of the predicted trajectories. We also adapt our approach for collision-free robot navigation among pedestrians based on noisy data and highlight the results in our simulator. |
[Downloads]
-
IJRR 2015 [Sagepub Link] [Bibtex] [PDF 3.05 MB]
-
WAFR 2011 (Preliminary version) [PDF 1.62MB]
[Online, Adaptive Motion Prediction]
 |
||
|
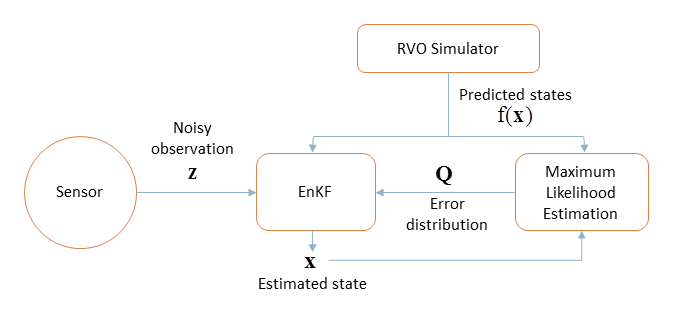
We estimate current state $(\mathbf{x})$ via an iterative process. Given noisy data observed by the sensor, RVO as a motion model, and the error distribution matrix $(\mathbf{Q})$, we estimate current state. The error distribution matrix $(\mathbf{Q})$ is recomputed based on the difference between the observed state and the prediction $f(\mathbf{x})$ and used to refine current estimation of $(\mathbf{x})$. |
||
 |
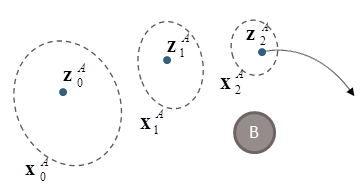 |
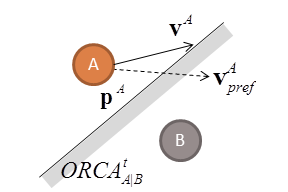
| (a) RVO State $(\mathbf{p}, \mathbf{v}, \mathbf{v}_{pref})$ | (b) Adaptive Refinement and Prediction |
| (a) Overview of RVO Simulation illustrating an agent’s position $(\mathbf{p})$, preferred velocity $(\mathbf{v}_{pref})$ and actual velocity $(\mathbf{v})$. If the ORCA collision-avoidance constraints prevent an agent from taking their preferred velocity, as shown here, the actual velocity will be the closest allowable velocity. These elements combine to form the RVO state $(\mathbf{x})$. (b) As new data is observed (blue dot) BRVO refines its estimate of a distribution of likely values of the RVO states (dashed ellipse). These parameters are then used with RVO to predict likely paths (as indicated by arrow). |
[Datasets used for our experiments]
 |
Campus Video data of students on campus recorded from the top of the ETH main building in Zurich was extracted by manual notation every 0.4 second. We extract three sequences from this data, each containing about 10 seconds of pedestrian interaction: Campus-1 (7 pedestrians), Campus-2 (18 pedestrians), Campus-3 (11 pedestrians). BIWI Walking Pedestrians dataset |
 |
Bottleneck Optical tracking equipment capture the motion of participant in a lab-environment. Participants moved through a bottleneck opening into a narrow passage. Data was collect with a passage width of 1.0 meter and 2.5 meter, denoted Bottleneck-100 and Bottleneck-250 respectively. Both studies have about 170 participants, and we use the data subsampled at a rate of 0.4 second. PeTrack Pedestrians data |
 |
Street This video is recorded from a street view, of low density pedestrian traffic, with manual motion tracking. The dataset contains motion of 148 pedestrians over a period of roughly 5 minutes. UCY "Crowds-by-Example" dataset |
 |
Student This video was recorded from a street view. The dataset contains the motion of 434 students over a period of roughly 3 minutes, tracked manually. UCY "Crowds-by-Example" dataset |
[Comparison with Offline Methods]
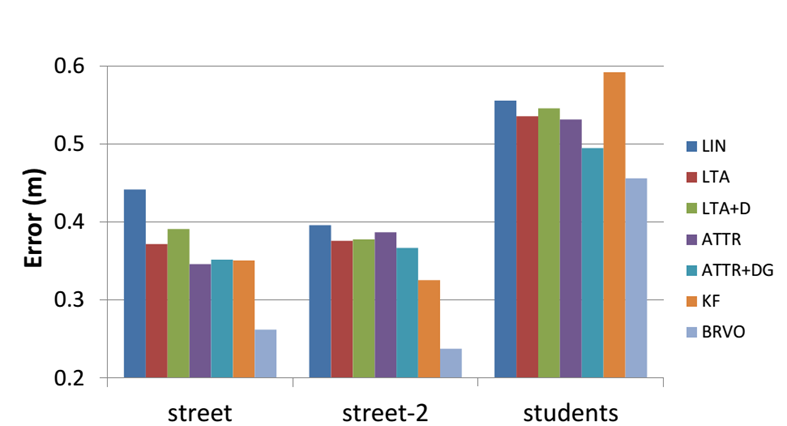
Comparison to State-of-the-art Offline Methods We compare the average error of LIN (linear velocity), LTA, ATTR, KF and BRVO. LTA+D and ATTR+DG indicate that they are used with ground-truth destination information (+D) and manually-annotated group information (+G). Our method outperforms KF, LTA and ATTR with an 18-40% error reduction rate over LIN in all three different scenarios. Significant improvement is made; compare the 4-16% and 7-20% error reduction rate of LTA and ATTR over LIN, respectively. |
||
 |
||
[BRVO for Robot Navigation]
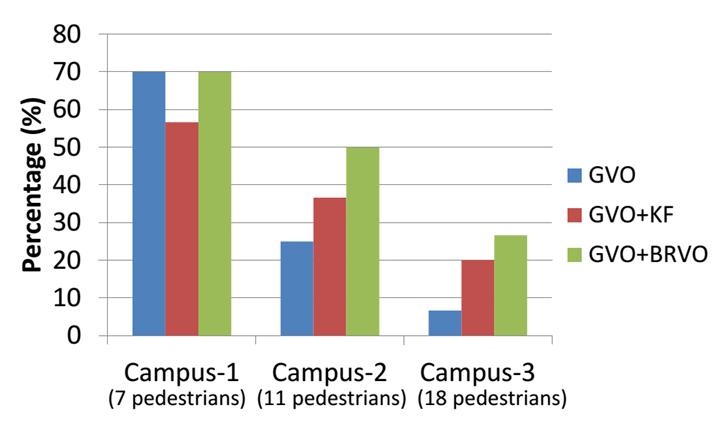
Performance of the robot navigation We measured the percentage of the trajectories in which the robot reached farther than halfway to the goal position without any collision during the data sequence, using only GVO (blue bars), GVO with KF (red bars), and GVO with BRVO (green bars), both with 15cm sensor noise. In many of these scenarios, using GVO for navigation often caused a robot to stop moving through the crowd to avoid collisions (the freezing robot problem). GVO-KF shows lower performance in very sparse scenario, but outperforms GVO-only method as the number of pedestrians increases. GVO-BRVO algorithm further improves the navigation, especially for more challenging scenarios with more pedestrians. |
||
 |
||
[Experiments]
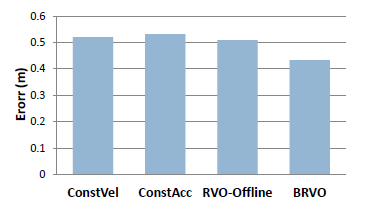
1) Learning individual, time-varying parameters BRVO produces less error than Constant Velocity and Constant Acceleration predictions. Additionally, BRVO results in less error than using a static version of RVO whose parameters were fitted to the data using an offline global optimization. |
||
 |
||
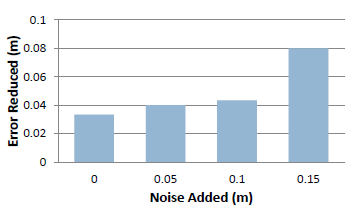
2) Learning maximum likelihood (EM) The improvement provided by the EM feedback loop for various amounts of noise. As the noise increases, this feedback becomes more important. |
||
 |
||
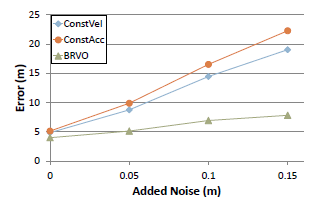
3) Noisy data Mean prediction error (lower is better). Prediction error after 7 frames (2.8s) on Campus dataset. As compared to constant velocity and constant acceleration models, BRVO can better cope with varying amount of noises in the data |
||
 |
||
|
Prediction accuracy (higher is better) (a-c) Shows prediction accuracy across various accuracy thresholds. The analysis is repeated at three noise levels. For all accuracy thresholds, for all noise levels BRVO produces more accurate predictions than constant velocity of acceleration models. The advantage is most significant for large amounts of noise in the sensor data as in (c) |
||
 |
||
4) Varying density scenario In high-density scenarios there is little motion and simple models such as constant velocity perform about as well as BRVO. However, in low and medium densities where there is more motion BRVO provides more accurate motion prediction than the other models. In general, BRVO performs consistently well across various densities. |
||
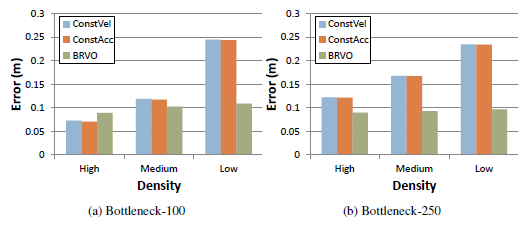 |
||
5) Varying sampling rates (a) As the sampling interval increases the error of Constant Velocity and Constant Acceleration estimations grows much larger than that of BRVO. (b) A comparison of prediction error with the recent approaches of LTA and ATTR on the same dataset. BRVO produces less error. |
||
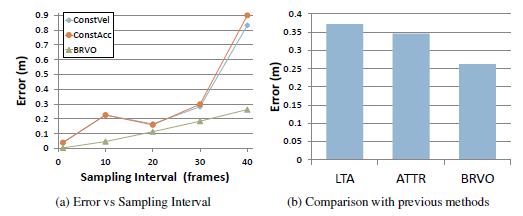 |
||