Lakulish Antani, Anish Chandak, Micah Taylor, Dinesh Manocha
We present a fast algorithm to perform sound propagation in complex 3D scenes. Our approach computes propagation paths from each source to the listener by taking into account specular reflections and higher-order edge diffractions around finite edges in the scene. We use the well known Biot-Tolstoy-Medwin diffraction model along with efficient algorithms for region-based visibility to cull away primitives and significantly reduce the number of edge pairs that need to be processed. The performance of region-based visibility computation is improved by using a fast occluder selection algorithm that can combine small, connected triangles to form large occluders and perform conservative computations at object-space precision. We show that our approach is able to reduce the number of visible primitives considered for sound propagation by a factor of 2 to 4 for second order edge diffraction as compared to prior propagation algorithms. We demonstrate and analyze its performance on multiple benchmarks.

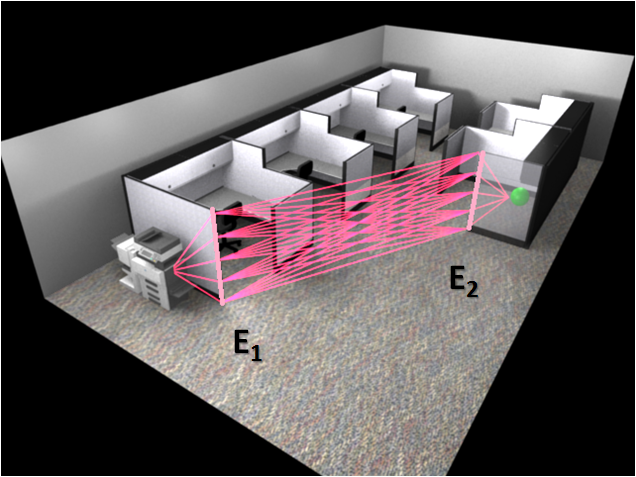
This image shows some second order diffraction paths computed in an office scene. The source is the printer, the listener is the green sphere. E1 and E2 are the two diffracting edges. Some of the diffraction paths are highlighted in the figure.
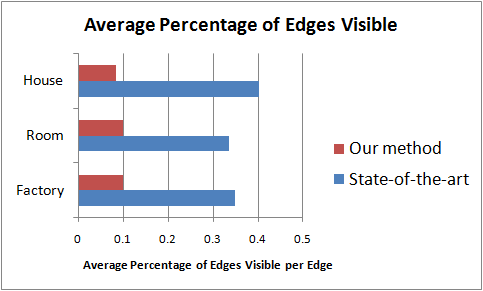
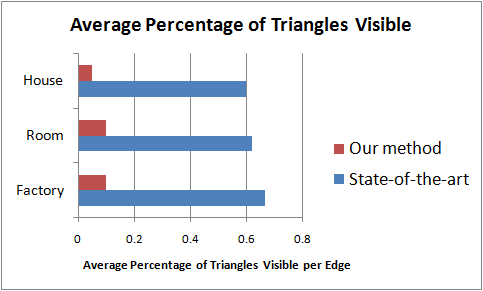
These plots show the advantage of using object-space accurate visibility algorithms to compute primitives visible from each diffracting edge in the scene. The state-of-the-art BTM implementation uses an overly conservative visibility culling algorithm, and therefore unnecessarily considers a large number of occluded diffraction paths.