Fast Proximity Computation Among Deformable Models using Discrete Voronoi Diagrams

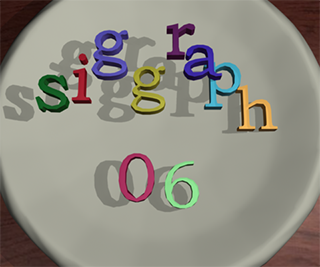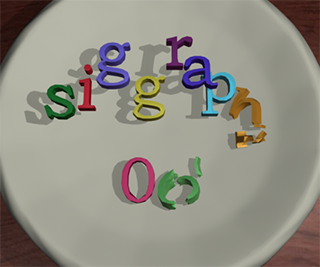Multiple Deformable Models Simulation #1

Multiple Deformable Models Simulation #2

Multiple Deformable Models Simulation #3

Multiple deformable models simulation: This sequence shows the positions of the objects at three time instances. The environment initially consists of 10 deforming objects represented using 5.5K triangles. As the simulation proceeds, the objects break into 25 sub-objects. Our algorithm is able to perform collision and separation distance computations, including self-collisions, among dynamically generated objects within 120 ms on a high-end PC.

Abstract

We present novel algorithms to perform collision and distance queries among multiple deformable models in dynamic environments. These include inter-object queries between different objects as well as intra-object queries. We describe a unified approach to compute these queries based on N-body distance computation and use properties of the second order discrete Voronoi diagram to perform N-body culling. Our algorithms involve no preprocessing and also work well on models with changing topologies. We can perform all proximity queries among complex deformable models consisting of thousands of triangles in a fraction of a second on a high-end PC. Our Voronoi-based culling algorithm can improve the performance of separation and distance queries by an order of magnitude.

Results


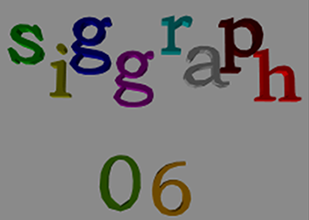
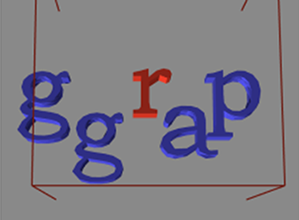
(a)	(b)	(c)	(d)

Application of our proximity query algorithm to a simulation with ten objects: (a) Position of 10 deforming objects: siggraph06. Our algorithm computes a 'Potential Neighboring Set' (PNS) of primitives for each primitive. (b)-(d) Stages in PNS computation. The red wireframe represents conservative bound on the separation distance between `r' and other letters. This bound is used to compute the PNS of `r'. (b) The object level PNS of letter `r' after stage I that uses AABB-based culling. (c) Object level PNS computed using our Discrete Voronoi Diagram based algorithm. (d) Zoomed view of feature level PNS between `r' and `g'. The exact distance tests are performed between red triangles in `r' and blue triangles in `g'. Total number of triangle pairs in feature level PNS=12K. Total computation time is around 60 ms per frame.

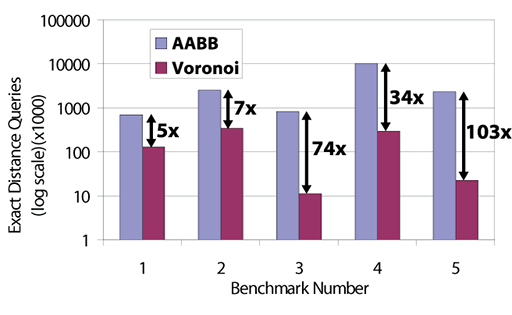
Culling efficiency of our algorithm: In this log-scale plot, we show the average number of exact triangle-triangle distance queries performed using an AABB-based algorithm and using Voronoi diagrams. We observe a 5-100 times higher culling efficiency using Voronoi diagrams on the five benchmarks. The high culling efficiency is due to the tight distance bounds obtained using the second order Voronoi diagrams.

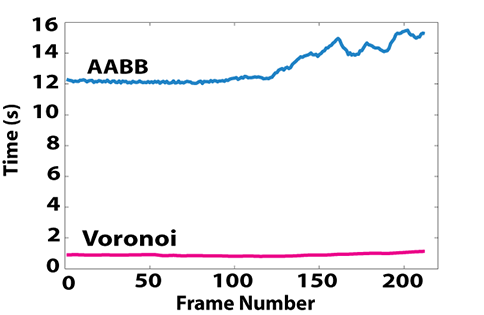
Performance improvement of our algorithm: This graph highlights the performance improvement obtained using our Voronoi-based algorithm over an efficient AABB-based algorithm on a deformable simulation with 200 objects. Due to the high culling efficiency obtained using Voronoi diagrams, we are able to achieve nearly one order of magnitude performance improvement over AABBs.

Publication

Video

Video (27 MB, DivX AVI): Video demonstrating proximity queries among multiple deformable models using Discrete Voronoi Diagrams. (Download DivX codec)

Related Work at UNC

Acknowledgements

RDECOM
Army Research Office
DARPA
National Science Foundation
Office of Naval Research