Simulation-Based Joint Estimation of
Body Deformation and Elasticity Parameters:

Abstract

Elasticity parameters are central to physically-based animation and medical image analysis. We present a general method to automatically estimate these parameters for a deformation simulator using an iterative optimization framework, given the desired (target) output surface/shape. During the optimization, the input model is deformed by the simulator, and the distance between the deformed surface and the target surface is minimized numerically. To accelerate the optimization process, we introduce a dimension reduction technique to allow a trade-off between the computational efficiency and desired accuracy. The reduced model is constructed using statistical training with a set of example deformations. To demonstrate this approach, we apply the computational framework to 2D animations of elastic bodies simulated with a linear finite element method. We also present a 3D elastography example, which is simulated with a reduced-dimension finite element model to improve the performance of the optimizer.

Results

Physically-Based Nonrigid Image Registration

Our method does not require any tedious process of parameter adjustment and is automatic once the segmentation of both the moving and the reference images are given. Compared to traditional optimization-based methods which minimizes image metrics and regularization terms, our method does not require a trade-off between image similarity and the quality of the deformation, since the deformation is always generated by a physically-based simulation.

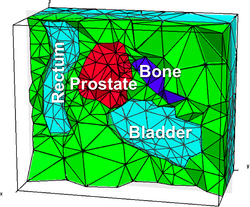
The tetrahedral mesh of the bladder-prostate- rectum area (left) and a close-up view of the three organs (right), where the white surface is the target prostate surface.

(a)
(b)
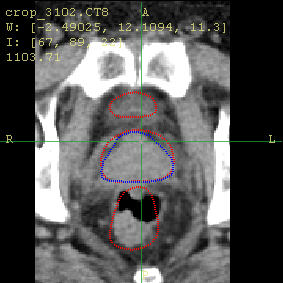
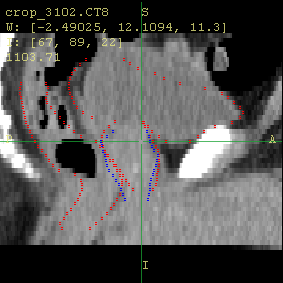
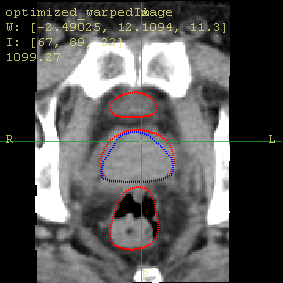
The axial and sagittal views of the moving image (a) before and (b) after the registration using our method. The red contours show the organ boundaries of the reference image, and the blue contours show the boundary of the prostate in the moving image. Notice how the organs move towards the red contour.

Physically-Based 2D Shape Deformation

In 2D shape deformation with a single material, the compressibility (Poisson’s ratio) is the main source of difference in deformed shape, if the same first-type boundary conditions are applied.

Example 2D shape deformations showing different deformation results with different Poisson’s ratios.

Given the source and target piecewise linear (represented by vertices and edges) shapes, the distance function to be minimized is based on distance between corresponding vertices. The error in the Poisson's ratio is about 10% in the test cases.

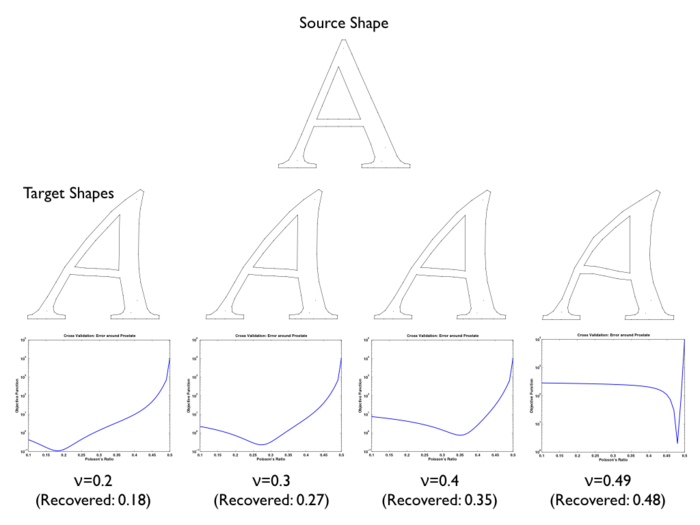Test of accuracy of the recovered Poisson’s ratios ν; the four target shapes are generated using four different ν values; for each subfigure, on the top is the target shape, and on the bottom is the plot of surface errors versus ν values.

Acceleration using Reduced Modeling

The degrees of freedom for the boundary forces in a typical 3D model is around 4,900, which makes the optimizer slow to converge (taking thousands of iterations). To improve the optimization, a dimension reduction is performed using linear bases trained using a PCA with 108 example deformations from CT images.

The first two principal components (visualized as nodal displacements on bladder and rectum surfaces) resulted from a PCA using 108 example deformations.

We observe better accuracy (in terms of surface distance and recovered elasticity values) and slower convergence with a larger number of bases used. Namely, the reduced bases provide a trade-off between the accuracy and the performance.

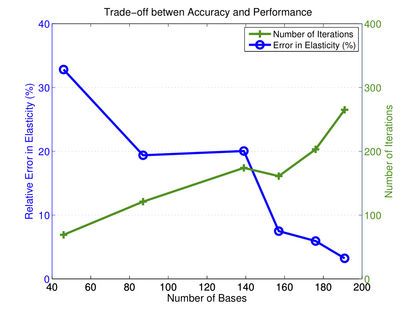
The number of reduced bases provides a means of trade-off between optimizer performance and accuracy of recovered elasticity values; the error (blue) decreases and the number of optimization iterations (green) increases with the number of bases used.

Publication

Huai-Ping Lee, Mark Foskey, Marc Niethammer, Pavel Krajcevski, and Ming C. Lin. 2012. Simulation-based joint estimation of body deformation and elasticity parameters for medical image analysis. IEEE Transactions on Medical Imaging vol. 31, no. 11, pp. 2156–2168, Nov. 2012. Preprint.

Huai-Ping Lee and Ming C. Lin. 2012. Fast Optimization-Based Elasticity Parameter Estimation Using Reduced Models. The Visual Computer, 28 (6-8):553–562.

Huai-Ping Lee, Mark Foskey, Marc Niethammer, and Ming Lin. 2010. Physically-based deformable image registration with material property and boundary condition estimation. In Proceedings of the 2010 IEEE international conference on Biomedical imaging: from nano to Macro (ISBI'10). [pdf]

Acknowledgments

We thank Ron Alterovitz and Ed Chaney for helpful discussions. We also thank Zijie Xu and Dr. Ron Chen for providing prostate patient CT data. This work was partially supported by Army Research Office, National Science Foundation, and Carolina Development Foundation.