 |
 |
 |
| Proximity Computations on Deforming Models: We use our interactive distance field computation for separation and penetration distance for dynamic simulation of deforming bunnies. Each bunny consists of 2K triangles and we compute localized distance fields on a 2563 grid for the simulation shown in this sequence. The average distance field and proximity query takes 120ms on a 3.2 GHz Pentium IV PC with NVIDIA GeForce 7800 GPU. | ||
We present an interactive algorithm to compute discretized 3D Euclidean distance fields. Given a set of piecewise linear geometric primitives, our algorithm computes the distance field for each slice of a uniform spatial grid. We express the non-linear distance function of each primitive as a dot product of linear factors. The linear terms are efficiently computed using texture mapping hardware. We also improve the performance by using culling techniques that reduce the number of distance function evaluations using bounds on Voronoi regions of the primitives. Our algorithm involves no preprocessing and is able to handle complex deforming models at interactive rates. We have implemented our algorithm on a PC with NVIDIA GeForce 7800 GPU and applied it to models composed of thousands of triangles. We demonstrate its application to medial axis approximation and proximity computations between rigid and deformable models. In practice, our algorithm is more accurate and almost one order of magnitude faster as compared to previous distance computation algorithms that use graphics hardware.
Results
 |
 |
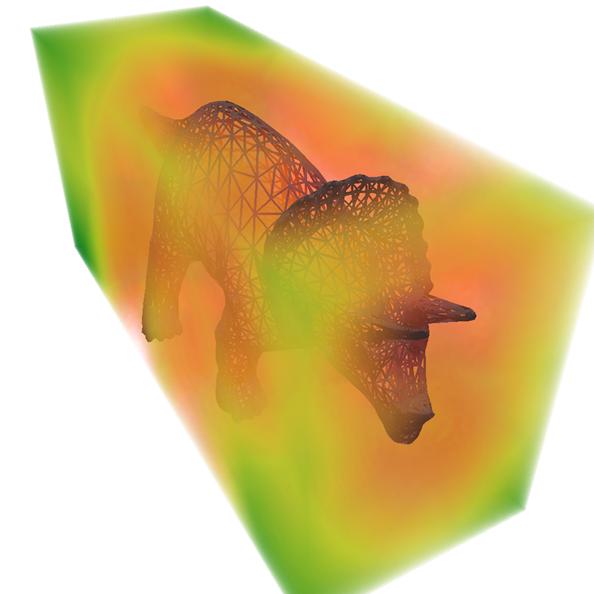
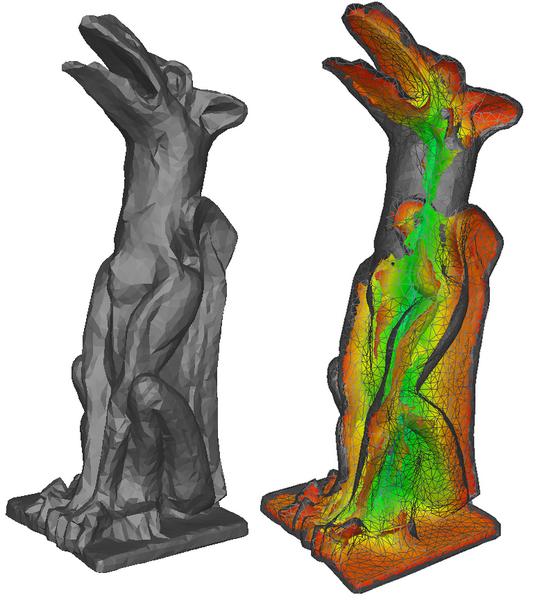
| 3D distance field computation: Computation of 3D distance field and discrete Voronoi diagram of Triceratops model (5660 polygons). Distance increases from red to green. Grid size = 255×111×84, Computation time = 768ms | Medial Axis Approximation: The left image shows the 11K Gargoyle model. The right image shows its simplified medial axis using our distance field algorithm. We use a grid of size 256×103×91 and the distance field computation takes around 625 ms on a 3.2 GHz Pentium IV PC with an NVIDIA GeForce 7800 GPU. |
DiFi: Fast 3D Distance Field Computation Using Graphics Hardware
Proximity Query and Collision Detection Research at the UNC Computer Science GAMMA Group.
Fast Computation of Simplified Medial
Axis