Robust Medial Axis research at UNC
The medial axis of a solid is the locus of the center of a
maximal sphere, as the sphere rolls around the object interior.
The locus is a central surface for the solid. The medial axis is
a kind of skeleton, and the closely related medial axis
transform is a complete shape representation based on the
skeleton.
For a 3-D polyhedral solid, the medial axis is composed of bisectors
of boundary features (the vertices, edges, and faces). These
bisectors are planes and quadric surfaces. The bisectors meet along
their intersection curves, which are degree-four algebraic space
curves. Computing an accurate medial axis requires reliable
computation with these curves and surfaces. Our method is based on
exact computation, which avoids some of the difficulties associated
with round-off error in geometric computation.
Current implementation results
|
Input complexity |
Output complexity |
Current running time |

Polyhedron 1 |
6 faces
9 edges
5 vertices
|
14 sheets
13 seams
4 junctions
|
10 seconds |

Polyhedron 2 |
16 faces
38 edges
24 vertices
|
69 sheets
88 seams
36 junctions
|
2.5 minutes |
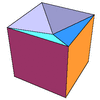
Dented box |
9 faces
16 edges
9 vertices
|
? sheets
56 seams
16 junctions
|
35 seconds |

Pizza box |
56 faces
124 edges
70 vertices
|
? sheets
2116 seams
946 junctions
|
23 minutes |
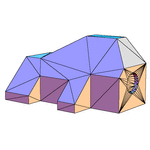
F-656 |
148 faces
222 edges
76 vertices
|
734 sheets
1091 seams
404 junctions
|
3.4 hours |
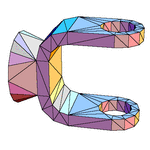
Bracket |
252 faces
378 edges
124 vertices
|
950 sheets
1439 seams
453 junctions
|
3.8 hours |
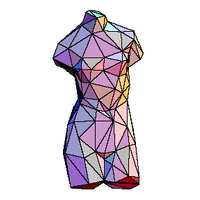
Venus de Milo |
250 faces
375 edges
127 vertices
|
1627 sheets
2223 seams
933 junctions
|
5.6 hours |
Star torus |
48 faces
72 edges
24 vertices
|
? sheets
190 seams
60 junctions
|
8 minutes |
Bagel |
104 faces
156 edges
52 vertices
|
745 sheets
1032 seams
437 junctions
|
18.5 minutes |
The implementation is a C++ program based on the MAPC library.
The medial axis images were rendered with Mathematica and
OpenGL.
Times are on an SGI MIPS R12000 processor. (Similar times have been
achieved on PCs running Linux.)
Applications
The medial axis transform is a fundamental shape operation with many
applications. It was proposed by Blum in 1967 for biological shape
measurement. It has also been used for path planning, automated
injection molding simulation, and feature recognition. One of the
best-known applications is finite-element mesh generation
[Srinivasan92, Sheffer98].
References
Tim Culver, John Keyser, Dinesh Manocha.
Accurate Computation of the Medial Axis of a Polyhedron.
Proc. Fifth Symposium on Solid Modeling and
Applications, pp. 179-190, 1999.
ckm-acmap-99
John Keyser, Tim Culver, Dinesh Manocha, Shankar Krishnan.
MAPC: A library for Efficient and Exact Manipulation of Algebraic
Points and Curves.
Proc. Fifteenth Annual Symposium on Computational Geometry,
pp. 360-369, 1999.
(An earlier version is available as UNC-CS Technical Report TR98-038. [compressed
Postscript])
kcmk-mapc-99
V. Srinivasan, L. R. Nackman, J.-M. Tang, S. N. Meshkat.
Automatic Mesh Generation Using the Symmetric Axis Transform of
Polygonal Domains.
Proc. IEEE, 80:9 (1992), pp. 1485--1501.
sntm-amgus-92
A. Sheffer, M. Etzion, A. Rappoport, M. Bercovier.
Hexahedral Mesh Generation Using Voronoi Skeletons.
Seventh International Meshing Roundtable, Michigan, October 1998.
Acknowledgements
Supported in part by an Alfred P. Sloan Foundation Fellowship, ARO
Contract DAAH04-96-1-0257, NSF Career Award CCR-9625217, ONR Young
Investigator Award (N00014-97-1-0631), Honda, Intel and NSF/ARPA
Center for Computer Graphics and Scientific Visualization.
Tim Culver
Last modified: Tue Sep 5 20:58:30 EDT 2000