Fast SVD on Graphics Processors

- Vinay Bondhugula, Naga Govindaraju and Dinesh Manocha

---

Abstract

This report discusses a GPU-based implementation of Singular Value Decomposition (SVD) and compares its performance with optimized CPU based implementations.

Introduction

Apart from the specific task they were designed for, present day GPUs can be used as powerful co-processors to perform general-purpose computation tasks. Although there has been prior work that makes use of GPUs for scientific computation, there has been very little work to use GPUs to solve general problems like SVD. SVD is a very fundamental problem that has numerous applications in search (Reference 5), scientific computing, statistics, signal processing, etc., which makes it very desirable to have a GPU based implementation of SVD.

Definition of SVD

If A is any m-by-n matrix, then there exists a factorization of the form



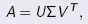
where 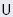is an m-by-m orthogonal matrix, 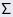is an m-by-n diagonal matrix and 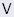is an n-by-n orthogonal matrix. Such a factorization is said to be the SVD of A.

Algorithm

There are two main stages in the SVD algorithm that we used:

• Bidiagonalization of the given matrix by applying a series of householder transformations (Refererence 2)
• Diagonalization of the bidiagonal matrix by iteratively applying the implicit-shifted QR algorithm (Reference 1 and Reference 2)

Bidiagonal Matrix:
A bidiagonal matrix has only two non-zero diagonals. The matrix is called upper bidiagonal if these are the main diagonal and the principal subdiagonal. Here's an example of an upper bidiagonal matrix:



Householder Transformations:
A householder transformation u = Hv, where H is symmetric, orthogonal and of the form

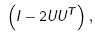
and u, and v are column vectors of length m, is a length preserving transformation that zeroes out m -1 elements of the column vector v below the first element. These transformations are alternately applied to the columns and rows to reduce any general matrix to a bidiagonal form. The entire series of transformations can be summed up as:

, where A is the original matrix, B is a bidiagonal matrix and P and Q are householder matrices.

Implicit-shifted QR Algorithm:
To perform the diagonalization of a bidiagonal matrix, the implicit-shifted QR algorithm is iteratively applied. Due to its iterative nature, this algorithm was found to be extremely slow on the GPU (when compared to CPU implementations) and hence we decided in favour of a hybrid approach, wherein the bidiagonalization would be performed on the GPU and diagonalization on CPU.

Brief Implementation Notes

• Matrices are represented as two-dimensional textures on the GPU.
• 4-component textures (RGBA) are used to store matrices.
• Frame Buffer Objects (FBO) are used for efficient off-screen rendering.
• Computation is performed by rendering quadrilaterals as large as the resolution of the output matrix.

Results and Conclusions

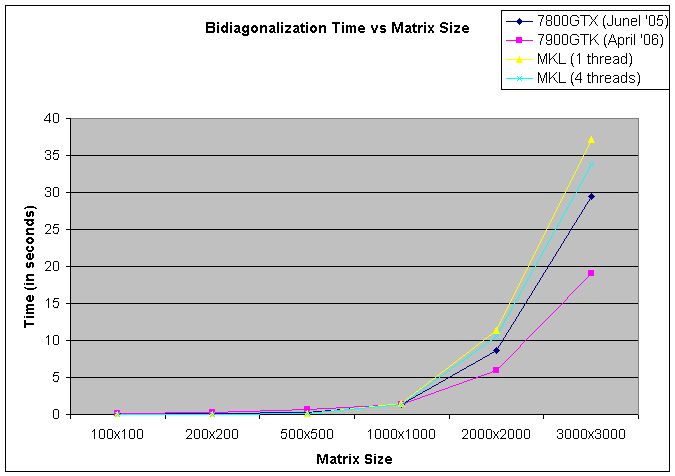
Our implementation was tested on two of the latest graphics cards (7900GTX and the 7800GTX) and these timings were compared with those of Intel MKL on a dual-Opteron CPU clocked at 2.8GHz. Although it's not entirely fair to compare our timings with those of Intel MKL's as our implementation does not save the transformation matrices during bidiagonalization, we nevertheless present Intel MKL's timings to give a general idea about the speed of current CPU-based implementations.
The first graph plots the time taken for bidiagonalization vs the matrix size. As our implementation uses a CPU-based diagonalization, we only consider the time taken for bidiagonalization.

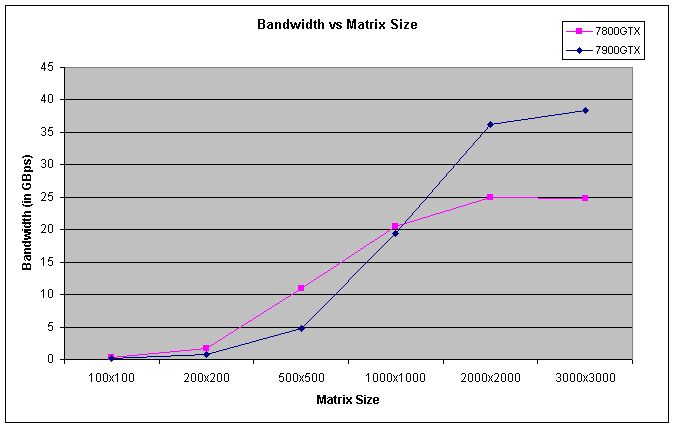
The second graph plots the observed bandwidth of our implementation vs the matrix size. The theoretical peak bandwidth of the 7900GTX is about 55GBps, so our implementation is able to get a fair throughput. It can be observed from the graph that the throughput is extremely low for matrices of smaller size. We believe that it is due to the delay introduced by Cg (the shader language that was used for writing fragment programs), which becomes negligble compared to the computation time for larger matrices.

References

1) J. W. Demmel and W. Kahan, Accurate Singular Values of Bidiagonal Matrices, SIAM J. Sci. Stat. Comput., 11 (1990), pp. 873-912.
2) J. H. Wilkinson and C. Reinsch, eds., Handbook for Automatic Computation, Vol 2.: Linear Algebra ,Springer-Verlag, Heidelberg, 1971.
3) P. Deift, J. W. Demmel, L.C. Li, and C. Tomei, The Bidiagonal Singular Values Decomposition and Hamiltonian Mechanics, SIAM J. Numer. Anal., 28 (1991), pp. 1463-1516.
4) Nico Galoppo, Naga K. Govindaraju, Michael Henson and Dinesh Manocha, LU-GPU: Efficient Algorithms for Solving Dense Linear Systems on Graphics Hardware, Proceedings of the ACM/IEEE SC 2005 Conference. Nov 12-18, 2005
5) David Gleich and Leonid Zhukov, SVD based Term Suggestion and Ranking System, ICDM 2004