Atul Narkhede and Dinesh Manocha
Department of Computer Science, University of North Carolina at Chapel Hill
Click here to get the C source.
Computing the triangulation of a polygon is a fundamental algorithm in computational geometry. In computer graphics, polygon triangulation algorithms are widely used for tessellating curved geometries, as are described by splines [Kumar and Manocha 1994]. Methods of triangulation include greedy algorithms [O'Rourke 1994], convex hull differences [Tor and Middleditch 1984] and horizontal decompositions [Seidel 1991].
This Gem describes an implementation based on Seidel's algorithm (op. cit.) for triangulating simple polygons having no holes (The code has since then been extended to handle holes). It is an incremental randomized algorithm whose expected complexity is O(n log*n). In practice, it is almost linear time for a simple polygon having n vertices. The triangulation does not introduce any additional vertices and decomposes the polygon into n-2 triangles. Furthermore, the algorithm generates a query structure that can be used to determine the location of a point in logarithmic time. Related gems include incremental Delaunay triangulation of a set of points [Lischinski 1994] and polygonization of implicit surfaces [Bloomenthal 1994].
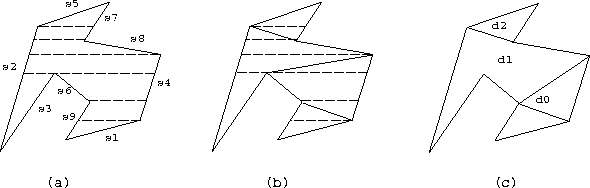
Generating monotone polygons from the trapezoid formation.
The algorithm proceeds in three steps as shown in Figure 1.
Let S be a set of non-horizontal, non-intersecting line segments of the polygon . The randomized algorithm is used to create the trapezoidal decomposition of the X-Y plane arising due the segments of set S. This is done by taking a random ordering s1 .. sN of the segments in S and adding one segment at a time to incrementally construct the trapezoids. This divides the polygon into trapezoids (which can degenerate into a triangle if any of the horizontal segments of the trapezoid is of zero length). The restriction that the segments be non-horizontal is necessary to limit the number of neighbors of any trapezoid. However, no generality is lost due to this assumption as it can be simulated using lexicographic ordering. That is, if two points have the same y-coordinate then the one with larger x-coordinate is considered higher. The number of trapezoids is linear in the number of segments. Seidel proves that if each permutation of s1 .. sN is equally likely then trapezoid formation takes O(n log*n) expected time.
A monotone polygon is a polygon whose boundary consists of two y-monotone chains. These polygons are computed from the trapezoidal decomposition by checking whether the two vertices of the original polygon lie on the same side. This is a linear time operation.
A monotone polygon can be triangulated in linear time by using a simple greedy algorithm which repeatedly cuts off the convex corners of the polygon [Fournier and Montuno 1984]. Hence, all the monotone polygons can be triangulated in O(n) time.
All the data-structures used in the implementation are statically allocated. The trapezoid formation requires a structure where the neighbors of each trapezoid and its neighboring segments can be determined in constant time. Therefore, for every trapezoid, the indices of its neighbors and the segments are stored in its table-entry T.
The query-structure Q, used to determine the location of a point, is implemented as described by Seidel. The same Q can be later used for fast point-location queries. Both Q and T are updated as a new segment is added into the existing trapezoid formation. This entails splitting in two the trapezoid(s) in which the endpoints of the segment lie, then traversing along the edge of the segment to merge in any neighboring trapezoids which both share the same left and right edges and also share a horizontal edge. All the monotone polygons are stored in a single linked list with pointers to the first vertex in the list stored in a table.
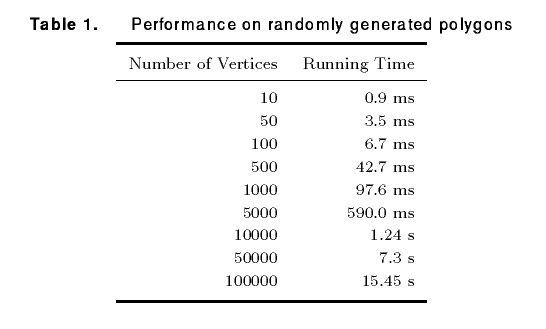
Table 1 shows the average running time of the algorithm for randomly generated data sets of various sizes. All the measurements were taken on an HP Series 735 with execution times averaged over one hundred repetitions.
Empirical testing has proven the method robust across wide class of input data. The present implementation uses an epsilon tolerance when testing for floating-point equality. This computation occurs when determining whether a point lies to the left (right) of a segment or when detecting coincident points. This tolerance could potentially be removed by substituting a well-crafted point-in-polygon test [Haines 1994].
The triangulation code is invoked through the main interface routine,
int triangulate_polygon(n, vertices, triangles);with an n-sided polygon given for input (the vertices are specified in canonical anticlockwise order with no duplicate points). The output is an array of n-2 triangles (with vertices also in anticlockwise order). Once the triangulated, point-location queries can be invoked as
int is_point_inside_polygon(vertex);additional details appear in the C source code which accompanies this Gem.