| Fast
Swept Volume Approximation of Complex Polyhedral Models Young J. Kim,
Gokul Varadhan, Ming C. Lin, and Dinesh Manocha,
ACM Symposium on Solid Modeling and Applications, June 16-20, 2003.
(Awarded
the best paper
at
the ACM Symposium on Solid Modeling and Applications 2003)
Acrobat (3.45 Mb)
|
|
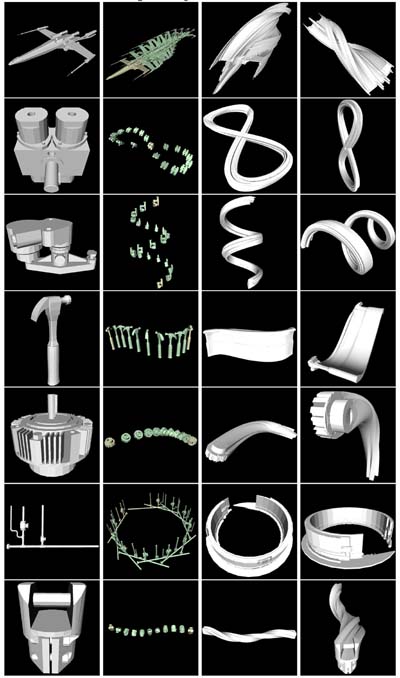
In each column, from left to right,
each figure shows a generator model, sweeping trajectory, and two views of the
resulting SV approximation reconstructed by our SV algorithm, respectively. In each row, each figure shows different benchmarking model,
from top to bottom, X-Wing, Air Cylinder, Swing Clamps, Hammer, Input Clutch, Pipe, and Pivoting Arms,
respectively.
|