Surface Distance Maps
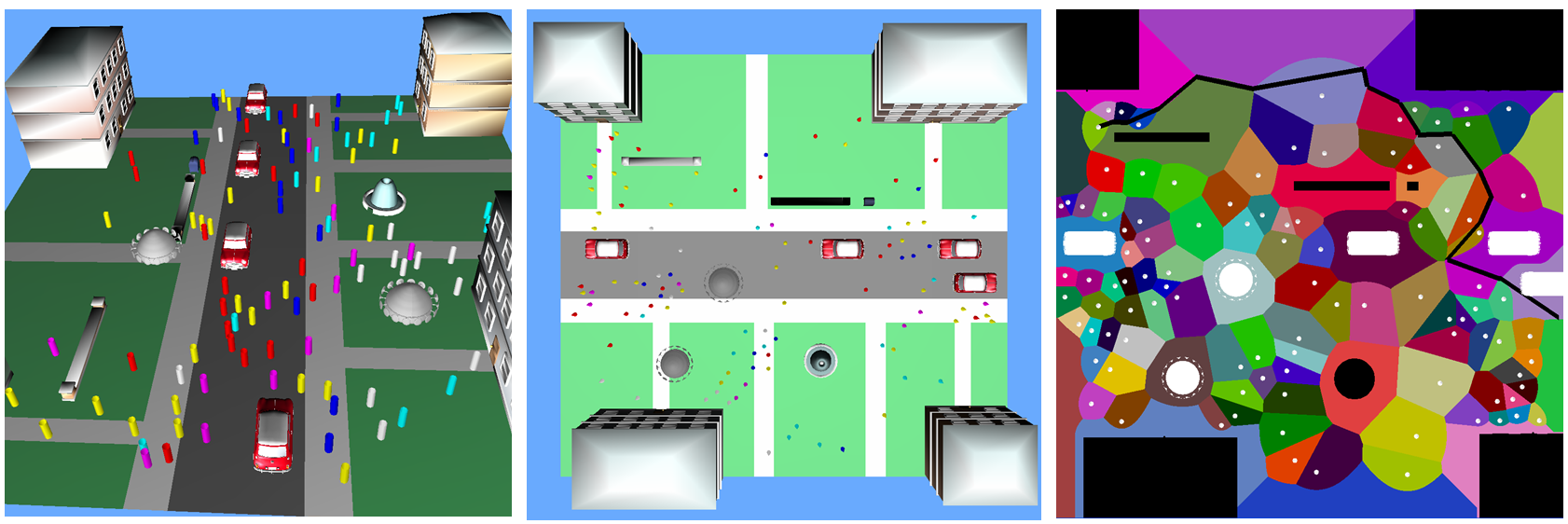 |
| Interactive motion planning
in a dynamic environment using surface distance maps, demonstrating
the motion of hundreds of human agents in a crowd simulation: (left-center)
Two views of the environment with dynamic 3D obstacles, including cars
and flying drones. Each human agent is represented as a cylinder and
colored by its goal. (right) The nearest neighbor map of the obstacles
and agents computed using surface distance maps. Each colored region
is closer to one 3D obstacle than to any other. The path for one agent
is shown using solid black lines. Our algorithm can perform the simulation,
including distance computations and path planning, for 100 agents at
10fps on a high-end PC. |
Abstract
We present a new parameterized representation called surface
distance maps for distance computations on piecewise 2-manifold
primitives. Given a set of orientable 2-manifold primitives, the
surface distance map represents the (non-zero) signed
distance-to-closest-primitive mapping at each point on a 2-manifold.
We present an interactive algorithm for computing the surface
distance map of triangulated meshes using graphics hardware. We
precompute a surface parameterization and use the parameterization
to define an affine transformation for each mesh primitive.
Our algorithm efficiently computes the distance field by applying
this affine transformation to the distance
functions of the primitives and evaluate these functions using
texture mapping hardware. In practice, our algorithm can compute
very high resolution surface distance maps at interactive rates and
provides tight error bounds on their accuracy. We use surface
distance maps for path planning and proximity query
computation among complex models in dynamic environments. Our
approach can perform planning and proximity queries in a dynamic
environment with hundreds of objects at intereactive rates and offer
significant speedups over prior algorithms.
Results
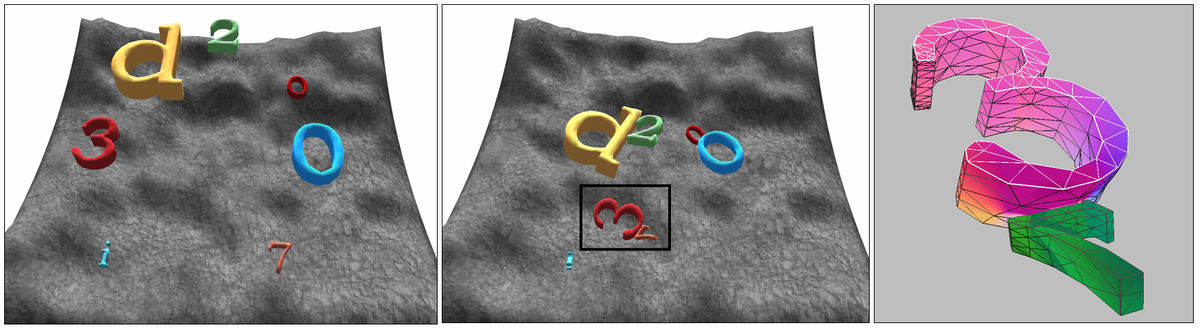 |
Surface Distance map computation
on deforming letters"i3d2007": Deforming dynamic
simulation on 7 letters falling on an uneven terrain, (6K triangles
total). (a)-(b) Two frames
from the simulation. (c) The gradient of surface distance maps
between two letters shows the direction of the closest point on
the other letter. Our algorithm can perform proximity queries
using high resolution surface distance maps of resolution 512 ×
512 in 100-200 ms per frame. |
Publication
Avneesh Sud, Naga Govindaraju, Russell Gayle, Erik Andersen and Dinesh Manocha Surface
Distance Maps Proc of Graphics Interface 2007.
Video
Video (DivX AVI): Video demonstrating computation
of Surface Distance Maps and application to proximity query computation.
(Download DivX codec if you have problems
playing the video using Windows Media Player)
related Work @ UNC-CH
Real-time Path Planning for Virtual Agents in Dynamic Environments
Fast Computation of Distance Fields and
Generalized Voronoi Diagrams Using Graphics Hardware
Fast Proximity Queries among Deformable Models Using Discrete Voronoi Diagrams
Proximity Query and Collision Detection
Research at the UNC Computer Science GAMMA Group.
UNC GAMMA Group
CB #3175, Department of Computer Science
University of North Carolina
Chapel Hill, NC 27599-3175
919.962.1749
geom@cs.unc.edu

